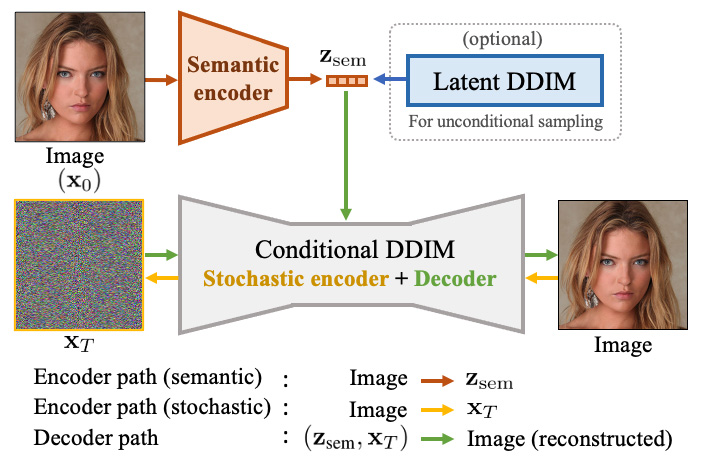
Diffusion Autoencoders: Toward a Meaningful and Decodable Representation

Konpat Preechakul Nattanat Chatthee Suttisak Wizadwongsa Supasorn Suwajanakorn

VISTEC - Vidyasirimedhi Institute of Science and Technology
Rayong, Thailand

CVPR 2022 (Oral)

Figure: Attribute manipulation and interpolation on real images. Diffusion autoencoders can encode any image into a two-part latent code that captures both semantics and stochastic variations and allows near-exact reconstruction. This latent code can be interpolated or modified by a simple linear operation and decoded back to a highly realistic output for various downstream tasks.

Abstract

Diffusion probabilistic models (DPMs) have achieved remarkable quality in image generation that rivals GANs'. But unlike GANs, DPMs use a set of latent variables that lack semantic meaning and cannot serve as a useful representation for other tasks. This paper explores the possibility of using DPMs for representation learning and seeks to extract a meaningful and decodable representation of an input image via autoencoding. Our key idea is to use a learnable encoder for discovering the high-level semantics, and a DPM as the decoder for modeling the remaining stochastic variations. Our method can encode any image into a two-part latent code where the first part is semantically meaningful and linear, and the second part captures stochastic details, allowing near-exact reconstruction. This capability enables challenging applications that currently foil GAN-based methods, such as attribute manipulation on real images. We also show that this two-level encoding improves denoising efficiency and naturally facilitates various downstream tasks including few-shot conditional sampling. Our novel latent space is more readily discriminative than StyleGAN-W (via inversion) when used to encode real input images.

Figure: Overview of our diffusion autoencoder. The autoencoder consists of a “semantic” encoder that maps the input image to the semantic subcode (x₀ → z_sem), and a conditional DDIM that acts both as a “stochastic” encoder (x₀ →x_T ) and a decoder ((z_sem, x_T)→ x₀). Here, zsem captures high-level semantics, while xT captures low-level stochastic variations, and together they can be decoded back to the original image almost exactly. To sample from this autoencoder, we fit a latent DDIM to the distribution of z_sem and sample (z_sem, x_T ∼N(0, I)) for decoding.

Paper

Code

Video (5 min.)

BibTex

@inproceedings{preechakul2021diffusion,
      title={Diffusion Autoencoders: Toward a Meaningful and Decodable Representation}, 
      author={Preechakul, Konpat and Chatthee, Nattanat and Wizadwongsa, Suttisak and Suwajanakorn, Supasorn},
      booktitle={IEEE Conference on Computer Vision and Pattern Recognition (CVPR)}, 
      year={2022},
}

Special thanks to Google Conference Scholarships for conference travel support.

Autoencoding quality / Varying stochastic subcode

Our diffusion autoencoder can reconstruct the input image almost exactly from the latent code that consists of two parts: semantic subcode and stochastic subcode. By varying the stochastic subcode and keeping the semantic subcode fixed, stochastic details of the decoded image change but the overall high-level structure remains the same.

Real input image Reconstructed Varying stochastic subcode Mean of the variation

Attribute manipulation on REAL images

To change a semantic attribute in an input image, we simply encode the input image to a latent code, add the vector corresponding to the target change, and decode it back. The results shown below do not involve any image blending or post-processing, and we only trained the autoencoder once and used it to manipulate all these different attributes. Unlike GANs, our method requires no inversion to manipulate real images and can well preserve the original details of the input image.
*Notice how adding eyeglasses comes with realistic shadows and removing ones undoes the refraction effect of the lens.

Real-image interpolation

To interpolate between two real images, we encode both images to their latent codes, compute a weighted sum of the codes, and decode the result back to an image. Both end points look ~exactly like the two input images, while the interpolation smoothly morphes between the two.

FFHQ-256

LSUN horse-128

LSUN bedroom-128

Unconditional Sampling

By fitting the latent distribution of our diffusion autoencoder with another diffusion model, we can also synthesize images unconditionally with competitive FID scores compared to a vanilla diffusion model. We show uncurated samples below.